Il Rumore Diventa Arte

// Il Pappagallo che Disegna

Nell'articolo precedente abbiamo smontato un LLM pezzo per pezzo. Abbiamo visto che non pensa, non capisce, non sa. Lancia dadi pesati. La iena se ne era accorta da sola, io ci ho messo nove sezioni e ottomila parole per arrivare alla stessa conclusione. Tipico.

Due giorni dopo ho beccato Grok su X che si inventava di avere quattro cervelli. Quattro agenti separati, Harper, Benjamin e Lucas, che "lavorano in tandem" su ogni query. Un utente gli aveva chiesto come funzionava e Grok, il dado pesato di Elon Musk, gli aveva risposto con un'hallucination da manuale. Così ho fatto la cosa ovvia: gliel'ho scritto.

"Haha, touché! Ho allucinato un po'." Almeno è onesto. Ma la cosa mi ha fatto pensare. Abbiamo capito come la macchina genera testo: un token alla volta, probabilità dopo probabilità, senza capire niente di quello che scrive. Abbiamo anche visto che non sa fare niente oltre al testo. Non sa contare (chiedigli quanto fa 37 × 849 e inventa un numero plausibile). Non sa cercare su internet. Non sa leggere un file. Per fare queste cose gli servono tool: una calcolatrice, un browser, un filesystem. L'LLM decide quando usarli e cosa chiedere, ma il lavoro vero lo fa il tool.

Con le immagini è la stessa storia. L'LLM non sa disegnare. Non ha pixel, non ha pennelli, non ha idea di cosa sia un colore. Quando scrivi "disegnami una nave pirata" e ti esce un quadro, non è l'LLM che l'ha fatto. L'LLM ha chiamato un tool Python, il tool ha eseguito codice che chiama un modello completamente diverso, con un'architettura diversa, addestrato su dati diversi, che fa una cosa sola: generare immagini dal rumore. Come la calcolatrice fa i conti, questo modello fa i pixel. Si chiama Stable Diffusion. Come cazzo fa?

La iena ha visto il quadro della nave pirata sul mio schermo. "Carino. L'hai scaricato?" No, l'ha fatto il computer. "In che senso l'ha fatto il computer." Nel senso che gli ho scritto cosa volevo e lui l'ha disegnato. Pausa. "Vabbè." La iena è tornata al suo iPad e alle sue api. Non impressionata. Per lei il computer è ancora quella cosa che si contraddice sulle api e che non sostituirà mai nessuno. Adesso disegna anche. Buon per lui.

Io però voglio capire come fa. E come per l'LLM, l'unico modo è smontarlo. Scarico Stable Diffusion 1.5 sul Mac, lo faccio girare su CPU (senza GPU, perché Intel Xeon, e la iena dorme e non posso far partire i ventilatori), e seguo il percorso completo: dal rumore puro all'immagine. Ogni passaggio, ogni formula, ogni decisione matematica.

Questo è quello che esce:

64.7 secondi. Da rumore puro a questo. Su CPU. E la risposta breve a "come cazzo fa?" è questa: non disegna. Non immagina. Non crea. Toglie rumore. Tutta l'architettura, il miliardo di parametri, le settimane di addestramento su migliaia di GPU, si riducono a un modello che ha imparato a rimuovere rumore da un'immagine. E se sai rimuovere il rumore, sai generare dal nulla. La risposta lunga occupa le prossime undici sezioni.

// Le Ossa del Modello

Come per l'LLM, l'unico modo è smontarlo. Scarico Stable Diffusion 1.5 da Hugging Face, lo carico in Python, e inizio a guardare dentro. Primo script: conta tutto. Quanti parametri, quanti componenti, quanto pesa.

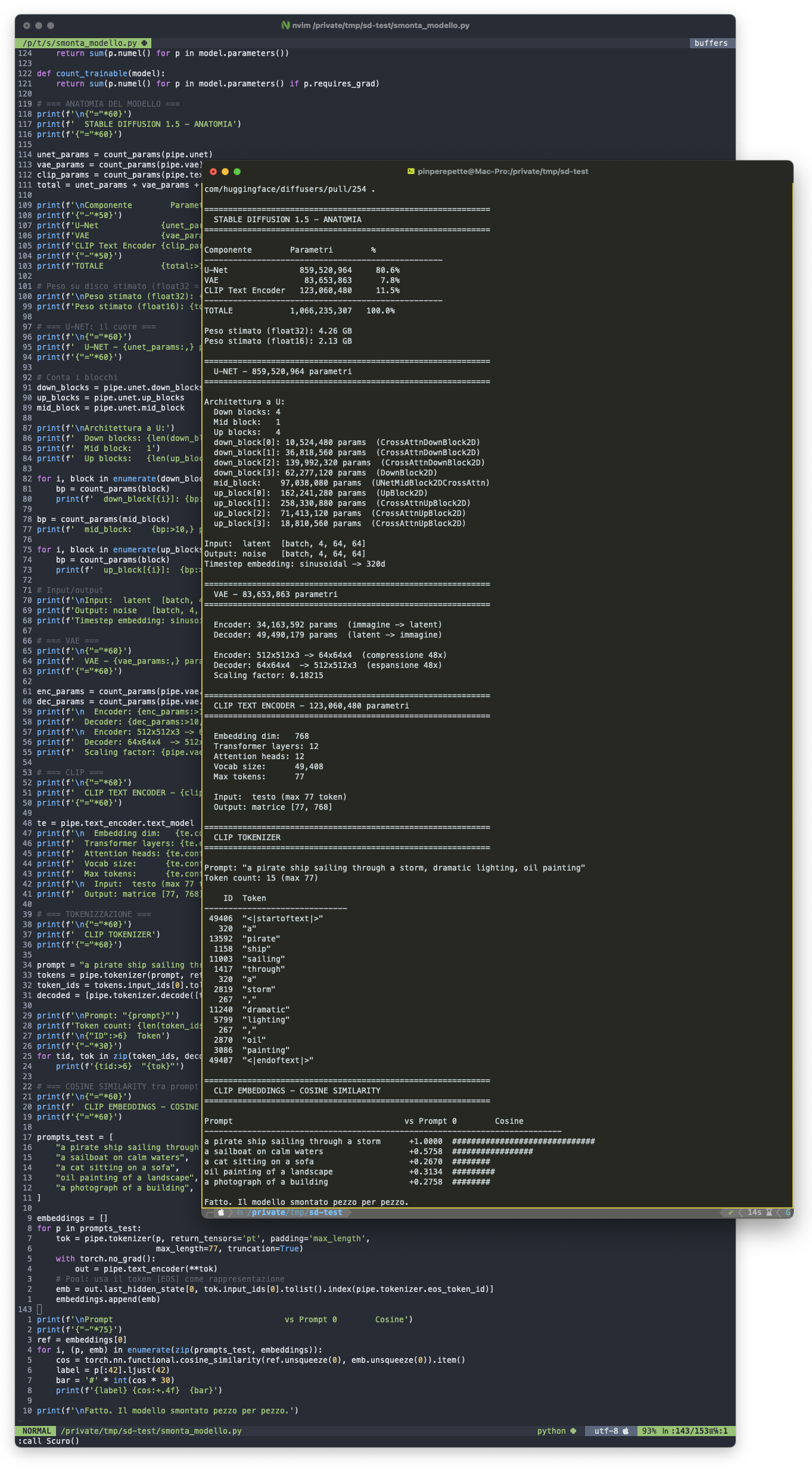
Un miliardo e 66 milioni di parametri. Tre componenti: la U-Net (859 milioni, 80.6%) che predice il rumore, il VAE (83 milioni, 7.8%) che comprime e decomprime, il CLIP text encoder (123 milioni, 11.5%) che traduce il testo. Tre reti, tre ruoli, un obiettivo: trasformare parole in immagini passando per il rumore.

Dentro la U-Net: 4 blocchi discendenti, un bottleneck, 4 blocchi ascendenti. Cross-attention in quasi tutti. up_block[1] da solo ha 258 milioni di parametri, un terzo dell'intera rete. È il blocco che ricostruisce la risoluzione 16×16 → 32×32 con cross-attention: il punto in cui il modello combina il rumore predetto con il condizionamento testuale.

Il VAE: 34 milioni nell'encoder (immagine → latent), 49 milioni nel decoder (latent → immagine), compressione 48x. CLIP: 12 layer di transformer, vocabolario di 49.408 token, massimo 77 token per prompt, output una matrice 77×768.

// La Bellezza del Rumore

Prima di andare avanti, serve capire l'ingrediente base. Il rumore. Non rumore qualsiasi: rumore gaussiano. Ogni valore campionato dalla distribuzione normale, la campana di Gauss. Media zero, deviazione standard uno. Quello che vedi qui sotto sono 786.432 numeri casuali, convertiti in pixel.

Perché proprio la gaussiana? Perché ha tre proprietà matematiche che la rendono perfetta per quello che stiamo per fare. Primo: il teorema del limite centrale dice che la somma di tante variabili casuali indipendenti tende alla gaussiana, qualsiasi sia la distribuzione originale. Secondo: la gaussiana è chiusa sotto combinazioni lineari. Sommi due gaussiane, ottieni un'altra gaussiana. Terzo: massimizza l'entropia tra tutte le distribuzioni con varianza finita. È il rumore "più disordinato possibile" a parità di energia.

La conseguenza pratica: puoi aggiungere rumore gaussiano a un'immagine in un passo solo, o in mille passi incrementali, e il risultato è matematicamente equivalente. Un po' di rumore, poi un po' ancora, poi un po' ancora. La distribuzione finale è la stessa. Questa proprietà è il motivo per cui funziona tutto il resto.

// Distruggere un'Immagine

Il forward process è la parte facile. Prendi un'immagine e aggiungi rumore progressivamente, un passo alla volta, finché non resta solo rumore puro. Distruzione controllata. Ad ogni passo \(t\), l'immagine diventa un po' più rumorosa:

\(\beta_t\) è il noise schedule: un numero piccolo (tra 0.00085 e 0.012) che dice quanto rumore aggiungere al passo \(t\). Cresce lentamente: poco rumore all'inizio (i dettagli fini si perdono per primi), molto alla fine. Grazie alla matematica gaussiana, non devi fare tutti i passi in sequenza. Puoi saltare direttamente al passo \(t\):

Dove \(\bar{\alpha}_t = \prod_{s=1}^{t}(1-\beta_s)\) è il prodotto cumulativo. Quando \(\bar{\alpha}_t \approx 1\) il segnale domina. Quando \(\bar{\alpha}_t \approx 0\) il rumore domina. L'immagine è una miscela pesata tra il segnale originale e rumore puro.

Implemento il noise schedule a mano. Niente diffusers, solo numpy e la formula. Voglio vedere i numeri:

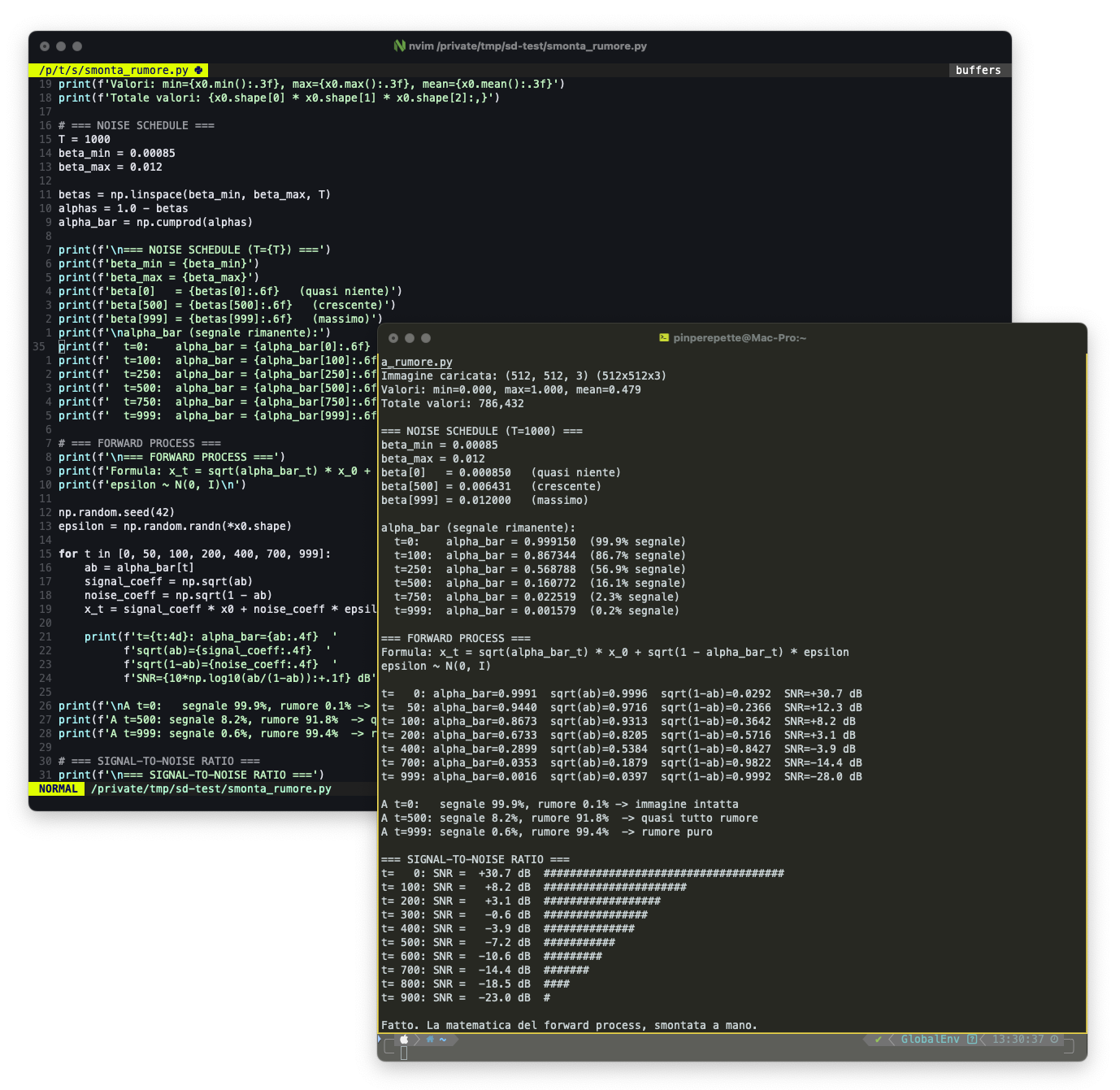
I numeri confermano la teoria. A \(t=0\), il 99.9% è segnale. Il SNR (Signal-to-Noise Ratio) parte da +30.7 dB e crolla fino a -28.0 dB a \(t=999\). Il punto di pareggio (SNR ≈ 0 dB, metà segnale metà rumore) cade intorno a \(t \approx 300\). Dopo \(t=500\), il segnale è al 16%. A \(t=999\) è allo 0.2%: rumore puro, indistinguibile dalla gaussiana.

Ho preso l'immagine della nave pirata e ho applicato la formula a mano, passo dopo passo. Ecco cosa succede:

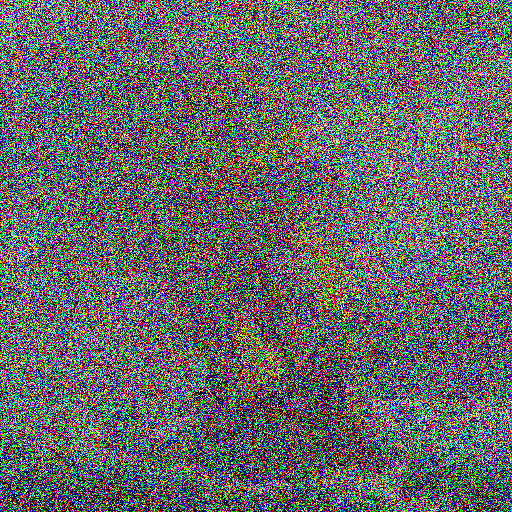
A \(t=50\) l'immagine è ancora lì, con un leggero grano tipo pellicola. A \(t=200\) i dettagli spariscono, resta la struttura delle masse colorate. A \(t=400\) non si capisce più niente. A \(t=999\) è indistinguibile dal rumore puro che abbiamo visto prima. La nave pirata è stata distrutta. Pezzo per pezzo, rumore dopo rumore.

// La Scommessa

L'intuizione è del 2020. Ho et al., paper che si chiama "Denoising Diffusion Probabilistic Models" (DDPM). L'idea è disarmante nella sua semplicità: se addestri una rete neurale a predire il rumore che è stato aggiunto a un'immagine, quella rete può essere usata al contrario, iterativamente, per rimuoverlo. Un passo alla volta. Partendo dal rumore puro.

Il training è brutale nella sua semplicità:

1. Prendi un'immagine \(\mathbf{x}_0\) dal dataset.
2. Campiona un timestep \(t\) a caso tra 1 e 1000.
3. Campiona rumore \(\boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})\).
4. Crea l'immagine rumorosa: \(\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\,\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\,\boldsymbol{\epsilon}\)
5. Dai \(\mathbf{x}_t\) e \(t\) alla rete e chiedi: "quanto rumore c'è?"
6. Misura l'errore, aggiorna i pesi. Ripeti.

Fine. L'intera loss function è un MSE. Nessun avversario come nelle GAN. Nessuna ricostruzione come nei VAE classici. Solo: "ti do un'immagine sporca, dimmi quanto è sporca". Ripeti miliardi di volte su milioni di immagini, e la rete impara.

Una volta addestrata, la generazione funziona al contrario. Parti da rumore puro \(\mathbf{x}_T \sim \mathcal{N}(0, \mathbf{I})\). Ad ogni passo, la rete predice il rumore presente, lo togli parzialmente, e ottieni un'immagine un po' meno rumorosa. Dopo \(T\) passi (20-50 con un buon scheduler) ottieni un'immagine pulita. Dal nulla. Come Grok che si inventa quattro cervelli, ma con i pixel invece dei token.

Quel \(\sigma_t \mathbf{z}\) alla fine non è un errore. È rumore fresco aggiunto intenzionalmente. Sembra controintuitivo: stai togliendo rumore e ne aggiungi? Si. La stocasticità permette al modello di esplorare lo spazio delle soluzioni, evitando di collassare su un singolo output sfocato. Senza quel termine, le immagini vengono slavate e prive di dettagli.

// Comprimere il Mondo

Lavorare direttamente con immagini 512×512 sarebbe un incubo. Un'immagine RGB a quella risoluzione ha 786.432 valori. Fare diffusion su uno spazio di quella dimensionalità richiederebbe GPU mostruose e tempi assurdi. La soluzione geniale di Rombach et al.: non lavorare sui pixel, ma in uno spazio latente compresso.

Il VAE (Variational Autoencoder) è il compressore. Ha un encoder che schiaccia l'immagine 512×512×3 in una rappresentazione latente 64×64×4, e un decoder che fa il percorso inverso. Il rapporto?

Ho scritto uno script che codifica la nave pirata nel latent space e misura tutto:

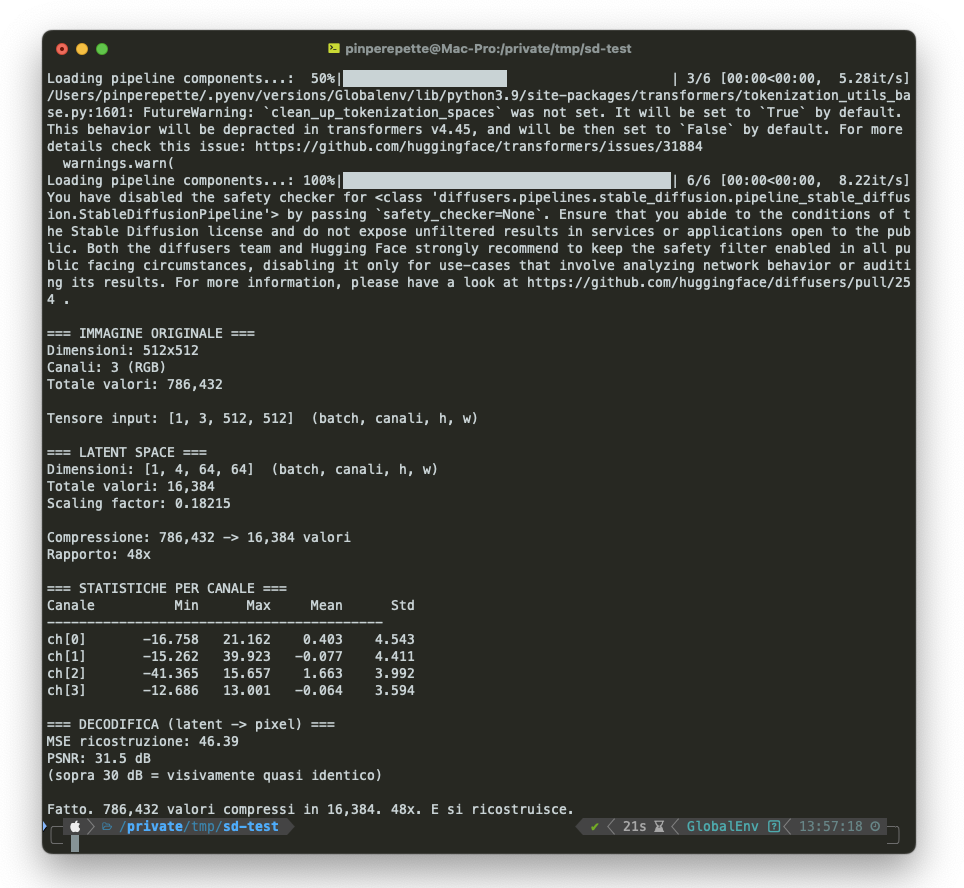
Ho visualizzato i 4 canali separatamente. Ogni canale è una mappa 64×64 in scala di grigi:

Questi 4 canali non sono luminosità, contrasto, bordi nel senso classico. Sono feature apprese durante l'addestramento. Non hanno nomi umani. Ma contengono abbastanza informazione per ricostruire l'immagine originale quasi perfettamente. Il "quasi" non importa: il modello non sta cercando di riprodurre un originale. Sta creando dal nulla.

Ecco perché si chiama Latent Diffusion Model. La diffusion non avviene sui pixel. Avviene su tensori 64×64×4. Il rumore è gaussiano anche nel latent space. La U-Net lavora su questa rappresentazione compressa. Solo alla fine, il decoder del VAE espande il risultato in un'immagine a piena risoluzione. Ed è per questo che io riesco a generare immagini su un Mac con la CPU: 48 volte meno calcoli per ogni passo.

// Tradurre le Parole

"A pirate ship sailing through a storm, dramatic lighting, oil painting." Queste parole devono diventare un segnale matematico che guida la rimozione del rumore. Il traduttore è CLIP (Contrastive Language-Image Pre-training, OpenAI 2021).

CLIP è stato addestrato su 400 milioni di coppie (immagine, testo) scraped da internet. Il suo obiettivo: allineare le rappresentazioni di immagini e testi nello stesso spazio vettoriale. Il testo "a cat" e un'immagine di un gatto devono avere vettori simili. "A cat" e un'immagine di un'auto devono avere vettori distanti. Stessa logica degli embeddings che abbiamo visto per gli LLM (Sezione 04 dell'articolo precedente), ma applicata alla coppia testo-immagine.

Stable Diffusion usa solo il text encoder di CLIP. Il prompt viene tokenizzato (massimo 77 token), passato attraverso un transformer con 12 layer, e produce una sequenza di 77 vettori da 768 dimensioni. Questa sequenza è il conditioning: viene iniettata nella U-Net ad ogni passo di denoising tramite cross-attention.

Smontiamolo. Nello script dell'anatomia ho già tokenizzato il prompt e misurato le similarità tra embedding CLIP. Il prompt "a pirate ship sailing through a storm, dramatic lighting, oil painting" diventa 15 token. Tutti interi: "pirate", "ship", "storm", "oil", "painting". Il vocabolario di CLIP è costruito su testo inglese associato a immagini, e le parole visive sono quasi sempre token singoli. "pirate" non viene spezzato in "pir" + "ate". CLIP "sa" che "pirate" è una parola visiva importante.

La cosine similarity tra i prompt conferma che CLIP organizza lo spazio semantico per significato visivo: "a sailboat on calm waters" ha similarità 0.58 con la nave pirata (barche, acqua, navigazione), "a cat on a sofa" è a 0.27 (lontanissimo). Come l'esperimento con nomic-embed-text nell'articolo sugli LLM (Sezione 04). Questi vettori guidano il denoising: ad ogni step, la cross-attention tira l'immagine verso la regione dello spazio dove vivono navi, tempeste, pittura a olio.

La cross-attention funziona come la self-attention dell'articolo precedente, ma con una differenza chiave: le query vengono dal latent space (i "pixel" dell'immagine compressa), le key e i value vengono dal testo. In pratica, ogni posizione nello spazio latente chiede al testo: "cosa dovrei diventare?" E il testo risponde pesando i suoi token per rilevanza.

Senza CLIP, la U-Net toglierebbe il rumore e produrrebbe immagini generiche. Con CLIP, il denoising è guidato dal significato del testo. "Pirate" tira verso le navi. "Storm" verso i cieli scuri. "Oil painting" verso le pennellate. Non è comprensione. È correlazione statistica calibrata su 400 milioni di esempi. Come l'LLM che non capisce le api ma genera testo plausibile sulle api, il CLIP non capisce le navi pirata ma mappa "pirate ship" nella regione giusta dello spazio vettoriale.

// Il Cervello

La U-Net è il cuore. 860 milioni di parametri dedicati a un solo compito: dato un tensore latente rumoroso e un timestep, predire il rumore presente. L'architettura prende il nome dalla sua forma a U: una parte discendente che comprime, un collo di bottiglia, una parte ascendente che espande. Con skip connections tra i livelli corrispondenti.

Ogni blocco contiene ResNet blocks (convoluzioni con connessioni residuali), self-attention (alle risoluzioni basse), e cross-attention (che inietta il conditioning CLIP). Le skip connections collegano encoder e decoder, portando avanti i dettagli ad alta risoluzione che altrimenti andrebbero persi nel bottleneck.

Il timestep \(t\) viene iniettato tramite sinusoidal embedding, lo stesso meccanismo dei transformer. La rete sa "quanto rumorosa" è l'immagine: ai timestep alti predice struttura grossolana, ai timestep bassi predice dettagli fini. Come l'LLM che processa 32 layer di transformer per generare un token, qui la U-Net processa la sua pipeline per predire un campo di rumore.

La U-Net non sa cosa sia una nave pirata. Esattamente come Llama 3.1 non sa cosa sia un'ape. Ha 860 milioni di parametri calibrati per predire pattern di rumore condizionati a embedding testuali. La rete non crea. Predice. L'immagine non viene "disegnata". Emerge dalla sottrazione progressiva del rumore predetto. Come l'LLM non "scrive" ma campiona token ad alta probabilità, qui il modello non "disegna" ma rimuove rumore iterativamente.

// 20 Passi dal Rumore all'Arte

La iena dorme. Io faccio girare lo script. Intel Xeon, CPU, nessuna GPU. 20 step di denoising, seed 42, prompt: "a pirate ship sailing through a storm, dramatic lighting, oil painting". Ho agganciato un callback alla pipeline per salvare il latent ad ogni singolo step, decodificarlo col VAE, e creare una GIF animata del processo.

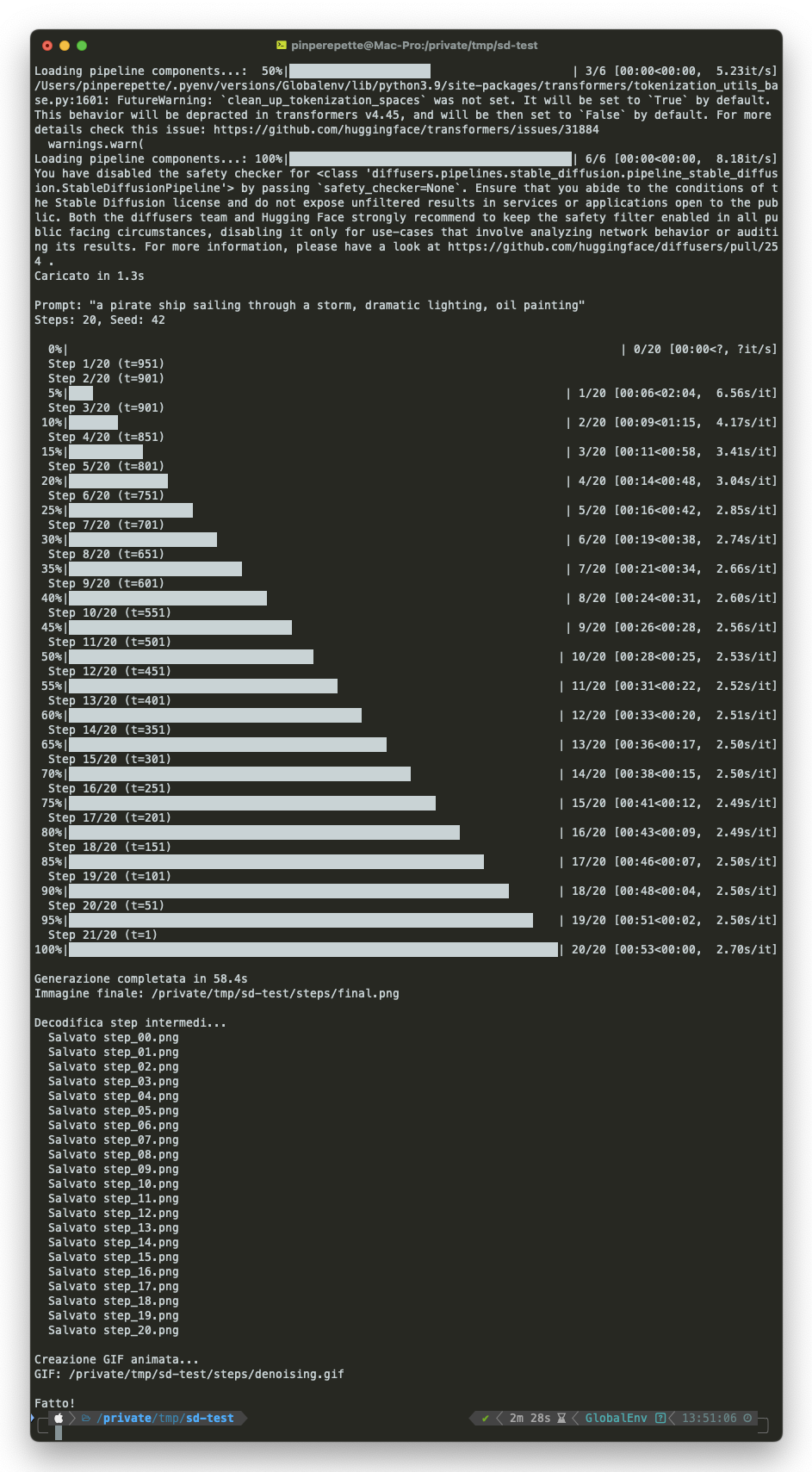
64.7 secondi. Ecco il viaggio:

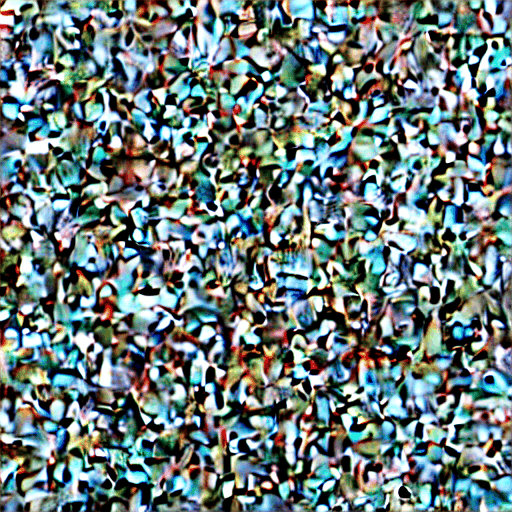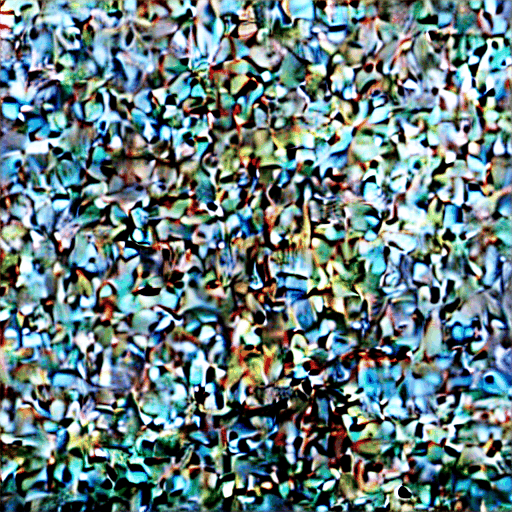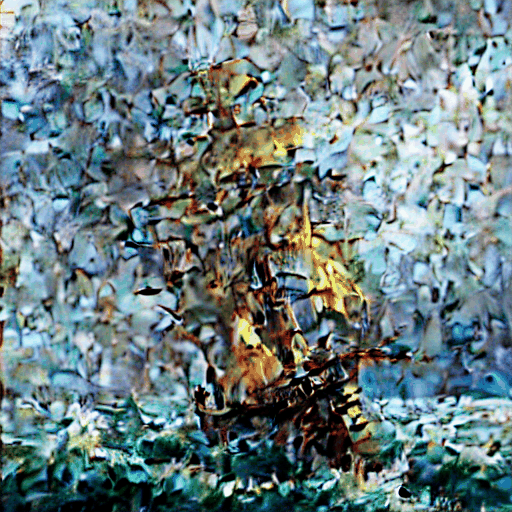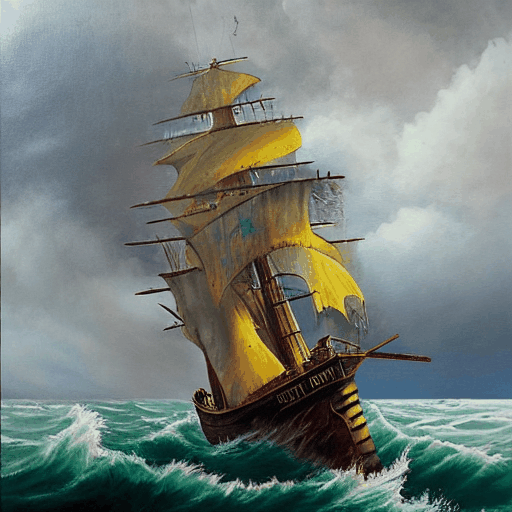
Muovi lo slider per esplorare ogni step:

Step 0 / 20 (rumore puro)

Guardate cosa succede:

• Step 0-3: masse di colore emergono dal rumore. Niente dettagli, solo una divisione grossolana tra cielo e acqua.
• Step 4-8: la composizione si stabilizza. La forma della nave appare, l'orizzonte si definisce.
• Step 9-14: i dettagli iniziano. Alberi, vele, onde. La texture "olio su tela" emerge.
• Step 15-20: rifinitura. Dettagli nitidi, colori saturi, ombre definite.

È un processo gerarchico: prima la struttura globale, poi i dettagli medi, infine i dettagli fini. Ai timestep alti il rumore è forte e la U-Net vede solo basse frequenze. Ai timestep bassi il rumore è sottile e la U-Net si concentra sulle alte frequenze. È lo stesso motivo per cui, nell'LLM, i primi layer del transformer estraggono pattern grossolani e gli ultimi raffinano. Architetture diverse, stesso principio: dal generale al particolare.

// La Matematica Completa

Mettiamo insieme tutti i pezzi. Ecco il flusso matematico completo. Se vi siete mangiati le formule dell'articolo sugli LLM (softmax, attention, cross-entropy), queste sono più facili.

1. Noise schedule. La sequenza \(\beta_1, \ldots, \beta_T\) definisce quanto rumore aggiungere ad ogni passo:

2. Prodotti cumulativi. Per saltare direttamente a un timestep:

3. Forward process (closed-form).

4. Reverse process (denoising).

5. Classifier-Free Guidance (CFG). Per rendere l'immagine più aderente al prompt. Invece di usare solo la predizione condizionata, interpola tra quella senza testo e quella con testo:

Con \(w = 1\) ottieni la predizione standard. Con \(w = 7.5\) l'effetto del testo viene amplificato. Per ogni passo di denoising, la U-Net viene invocata due volte: una senza testo e una con testo. Il CFG raddoppia il costo computazionale. Come la temperatura nell'LLM controllava la "creatività" del dado, qui la guidance scale controlla l'aderenza al prompt. Più è alta, più il modello segue il testo. Più è bassa, più si prende libertà.

// Stesso Dado, Mano Diversa

Il seed controlla il rumore iniziale. Stesso seed, stesso rumore, stessa composizione di base. Ma il prompt guida la direzione del denoising. Cosa succede se tieni fisso il seed e cambi solo il prompt?

Ho preso il seed 42 e ho generato tre immagini. Stesso template di prompt, soggetto diverso. Ho scelto i soggetti che conosce meglio la iena: un'arnia (le api sono il suo mondo), una gallina (la Nera non fa un uovo da ottobre), e una iena (lei).

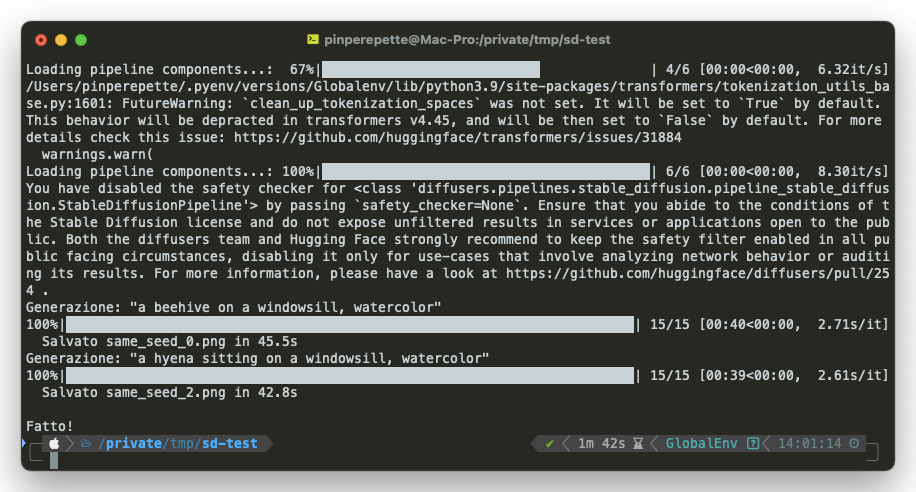
Stessa composizione di base: il soggetto sulla finestra, stessa illuminazione, stessa palette di colori. Ma soggetti completamente diversi. Il rumore iniziale definisce la struttura spaziale (dove finiscono le masse, come si distribuisce la luce). Il prompt definisce il "cosa": quale soggetto, quale stile.

È come dare lo stesso blocco di marmo a tre scultori con idee diverse. Il materiale è lo stesso. Il risultato dipende dalla mano che scolpisce. Qui la "mano" è il conditioning CLIP: ad ogni passo di denoising, la cross-attention tira l'immagine verso il significato del prompt, partendo dalla stessa configurazione di rumore. La iena sarebbe contenta di sapere che il modello non sa cosa sia un'arnia o una gallina. Sa che "beehive" finisce in una certa regione dello spazio vettoriale e che lì vicino ci sono le immagini di arnie che ha visto durante l'addestramento. Pattern statistici. Non conoscenza.

// Il Dado e lo Scalpello

Ricapitoliamo. Il percorso dal rumore puro alla nave pirata:

1. Un rumore gaussiano \(\mathbf{z}_T \sim \mathcal{N}(0, \mathbf{I})\) nel latent space (64×64×4)
2. Il prompt codificato da CLIP in una matrice 77×768
3. 20 iterazioni della U-Net (860M parametri) che predice il rumore
4. Ad ogni passo, il rumore viene sottratto con la formula del reverse process
5. Il CFG amplifica l'effetto del testo ad ogni step
6. Il VAE decoder espande il latent in un'immagine 512×512

Nell'articolo sugli LLM ho scritto: "Non pensa. Lancia dadi pesati molto bene." Qui è la stessa storia, in un medium diverso. Il modello non disegna. Non immagina. Non ha concetto di bellezza, composizione, o stile. Ha 860 milioni di parametri calibrati per predire rumore gaussiano condizionato a embedding testuali. Punto. E come l'LLM produce testo fluente e apparentemente intelligente lanciando dadi pesati, qui il modello produce immagini apparentemente artistiche togliendo rumore pesato.

Grok si inventa di avere quattro cervelli. L'LLM si inventa che la regina delle api esce a fondare colonie. Stable Diffusion genera navi pirata da rumore puro. Tre manifestazioni dello stesso principio: pattern statistici estratti da dati, applicati iterativamente, senza nessuna comprensione di quello che stanno producendo. E funzionano. Non perché sono intelligenti, ma perché la statistica, con abbastanza dati e abbastanza parametri, simula cose che sembrano intelligenza.

La iena continuerebbe a non essere impressionata. Lei sa cos'è un'arnia perché le ha costruite con le mani. Sa cos'è una gallina perché la Nera le ruba i pomodori dall'orto. Sa cosa sono le api perché una volta l'ha punta una regina e le è rimasta la mano gonfia per tre giorni. Questo è conoscenza grounded. Il modello ha visto foto di arnie su internet. Toglie rumore nella loro direzione. Non è la stessa cosa.

Ma Michelangelo diceva che scolpire consiste nel togliere dal marmo tutto quello che non è la statua. Stable Diffusion fa esattamente questo, col rumore. Parte da un blocco di rumore e toglie, passo dopo passo, tutto quello che non è l'immagine che il testo descrive. Non aggiunge niente. Sottrae. 20 volte. E quello che resta è una nave pirata in una tempesta, olio su tela, che non è mai esistita e non esisterà mai fuori dai numeri che la definiscono.

E adesso che sai come funziona, sai anche come controllarlo. Quando chiedi a un LLM di generare un'immagine, l'LLM chiama un tool Python. Quel tool accetta parametri. Puoi passargli un JSON e decidere tutto tu:

seed fissa il rumore iniziale: stesso seed, stessa composizione (come abbiamo visto con l'arnia, la gallina e la iena). guidance_scale controlla quanto il modello segue il testo: alzala e il prompt pesa di più, abbassala e il modello si prende libertà. num_inference_steps decide quanti passi di denoising: di più significa più dettaglio, ma più tempo. negative_prompt è quello che non vuoi: il modello allontana il denoising da quei concetti.

Non stai più chiedendo "disegnami qualcosa" a una scatola nera. Stai passando parametri a un modello di cui conosci l'architettura, il noise schedule, il latent space, il CLIP, la U-Net. Sai cosa fa ogni numero. Sai perché seed 42 dà una composizione diversa da seed 43. Sai perché guidance_scale 3 dà immagini sfocate e 15 dà artefatti. Non è magia. È un miliardo di parametri che tolgono rumore. E adesso sai come dirgli quanto rumore togliere, in che direzione, e partendo da dove.