// La Cena di San Valentino
Sezione 01. L'antefattoSan Valentino. 26 anni di matrimonio. La iena ed io a cena fuori, come due persone normali. Lei non ha nemmeno il telefono. Anzi ce l'ha, da qualche parte in fondo alla borsa, spento o scarico, non si sa, non le interessa. È una delle ultime persone al mondo che esce di casa senza controllare se ha il telefono addosso. Io invece ce l'ho in tasca, vibrante, con le notifiche di Twitter che si accumulano come pacchetti in un buffer pieno.
Stiamo parlando. Cioè, lei sta parlando. Delle api. La iena si è data all'apicoltura anni fa e da allora le api sono diventate l'argomento dominante di qualsiasi conversazione, pasto, viaggio in macchina e, a quanto pare, cena di San Valentino. Le api stanno bene. Le api hanno fatto il primo volo di pulizia. La regina nuova è promettente. Io annuisco con la frequenza giusta, circa 0.3 Hz, un cenno ogni tre secondi, sufficienti a simulare attenzione attiva.
"Ti ricordi quella pianta che avevamo messo nell'orto l'anno scorso?" No. Non mi ricordo. Non ricordo nemmeno cosa ho mangiato a pranzo. Ma annuisco. 0.3 Hz. Costante. Lei passa dall'orto alle galline. Abbiamo delle galline in montagna. Le galline stanno bene. La Bionda ha ricominciato a fare le uova. La Nera no, la Nera è una delusione, non fa un uovo da ottobre. Annuisco. Non me ne frega veramente un cazzo, ma dopo 26 anni ho perfezionato la faccia di chi ascolta con trasporto.
Poi succede la cosa. In sottofondo, tra il rumore dei piatti, le cinquanta conversazioni simultanee, i camerieri che gridano ordini e la macchina del caffè che sembra un motore a reazione, sento una canzone. Quei primi accordi al piano, quella voce. La conosco. L'ho sentita mille volte. Ma il titolo non mi viene. La classica tortura cognitiva che ti mangia il cervello per il resto della serata.
La iena sta spiegando la differenza tra l'ape ligustica e la carnica. O forse è passata alle potature. Non sono sicuro. Ma il mio cervello ha già cambiato contesto, un context switch involontario, come un thread ad alta priorità che interrompe il main loop. Devo sapere che canzone è.
"Scusa un secondo."
Lo sguardo della iena è un pacchetto ICMP con TTL=1. Ma io ho già il telefono in mano. Apro Shazam. Il ristorante è un muro di rumore: 50 persone, posate su ceramica, "TAVOLO SETTE!", il frullatore del bar, e la iena che ha smesso di parlare di api per guardarmi con un'intensità che nessun microfono potrebbe catturare. Premo il pulsante. Cinque secondi. "I Will Always Love You", Whitney Houston.
Whitney Houston. 1992. Al ristorante, a San Valentino, mentre la iena mi parla delle api e io tiro fuori il telefono. "I Will Always Love You". L'ironia è talmente perfetta che nemmeno un algoritmo avrebbe potuto inventarla.
"Ecco! Whitney Houston!" dico, come se avessi appena risolto un teorema. La iena mi guarda con un'espressione che in 26 anni ho imparato a classificare come threat level: elevated. Rimetto il telefono in tasca. "Scusa, dimmi. Le api."
La cena prosegue. Le api. L'orto. La Nera che non fa le uova. La iena mi perdona, più o meno, perché dopo 26 anni sa che sono recuperabile ma non modificabile. Io fingo di aver dimenticato. Ma non ho dimenticato un cazzo. La domanda è già lì, piantata nella corteccia prefrontale come un processo zombie che non puoi killare:
Come cazzo ha fatto?
Il viaggio di ritorno a casa. Guido. La iena continua a parlare, adesso è passata alla figlia. Che domani deve andare a fare dei lavori da Serena. Che ha comprato una borsa nuova. Che quella gonna non le stava bene. Io annuisco. 0.3 Hz. Ma non sto ascoltando. Sto pensando a Shazam.
"Sei d'accordo?" chiede la iena.
"Assolutamente" rispondo, senza la minima idea di cosa abbia appena accettato. Potrei aver dato il consenso a comprare altre dieci galline, ad allargare l'orto, a un terzo apiario. Non importa. Il mio cervello è già su un'altra frequenza. Letteralmente.
50 persone che parlano. Piatti. Caffè. L'ape ligustica e la carnica. La Nera e le sue uova mancanti. La voce della iena che copriva almeno 20 dB di banda utile. E un'app, in 5 secondi, ha identificato una canzone tra 70 milioni di tracce, da un segnale sommerso nel rumore. Ha guardato 5 secondi di caos acustico e ha detto "è questa, al secondo 95 del brano originale, con uno sfasamento temporale di 0.00008 secondi". Come cazzo ha fatto?
Shazam non sente la canzone. Non la "ascolta" in nessun senso umano del termine. Cattura 44100 numeri al secondo dal microfono, li tritura con trasformate, ne estrae un'impronta digitale, la spedisce a un server, e in meno di 5 secondi riceve indietro titolo, artista, album, copertina e link ad Apple Music. In un ristorante pieno. Con la iena che parla. In un frastuono in cui io non riuscivo nemmeno a ricordare il titolo, e io la canzone la conoscevo.
Mi chiudo in ufficio. La iena dorme. Io no.
// I Tentativi
Sezione 02. Intercettare il traffico di ShazamIl primo istinto del pirata: intercettare il traffico. Vedere cosa manda l'app al server, cosa torna indietro, leggere i byte. Per farlo serve un man-in-the-middle: mettere un proxy tra il telefono e il server di Shazam.
I telefoni di casa
Apro il cassetto dei muletti. Due Apple e nessun Android, l'ho usato settimana scorsa, dove cazzo l'ho messo. Nessuno dei due è jailbreakabile. iOS recente, bootchain locked, exploit chain chiusa. Per intercettare HTTPS servono certificati custom installati come root CA, e senza jailbreak o root non c'è modo di bypassare il certificate pinning di Shazam. Primo tentativo, prima parete.

L'emulatore Android
Piano B: emulare. Emulatore Android su Mac, Shazam installato, mitmproxy come proxy HTTPS, Frida per hookare il certificate pinning a runtime. Il setup funziona: l'emulatore parte, Shazam si installa, mitmproxy cattura il traffico. Vedo le richieste a googleapis.com, facebook.com, app-measurement.com. L'app è una festa di tracker. Ma la request che mi interessa, quella verso amp.shazam.com/match, non arriva mai.

Il certificate pinning
Shazam usa OkHttp3 CertificatePinner con pinning su tre domini: amp.shazam.com, cdn.shazam.com e *.music.apple.com. L'app accetta solo certificati specifici, hardcoded nel codice. Il certificato di mitmproxy viene rifiutato. Con Frida scrivo uno script che hooka le classi Java di verifica SSL e disabilita il pinning. Funziona. Il traffico HTTPS ora passa dal proxy. Ma Shazam crasha prima di generare il fingerprint.
Il crash di Frida
Il problema è più in basso. L'emulatore gira su x86_64, ma libsigx.so, il motore di fingerprinting nativo di Shazam, è compilato per ARM64. L'NDK Translation Layer tenta di tradurre le istruzioni ARM in x86 al volo. Ma quando libsigx.so esegue operazioni FPCR (Floating Point Control Register specifico di ARM64), il traduttore va in panico:
Le istruzioni ARM64 per il controllo della precisione floating point non hanno equivalente diretto in x86. Il fingerprinting muore. Nessun fingerprint, nessuna request al server, niente da intercettare. Secondo tentativo, seconda parete.
La decompilazione dell'APK
Non potendo intercettare il traffico live, prendo l'altra strada: decompilare l'APK. Estraggo il bytecode smali con apktool per leggere le classi Java, e per il binario nativo libsigx.so (il motore di fingerprinting ARM64) apro Aether, un disassembler per macOS che ho scritto io. Se non posso vedere il traffico in transito, posso almeno leggere il codice che lo genera. Le classi chiave:
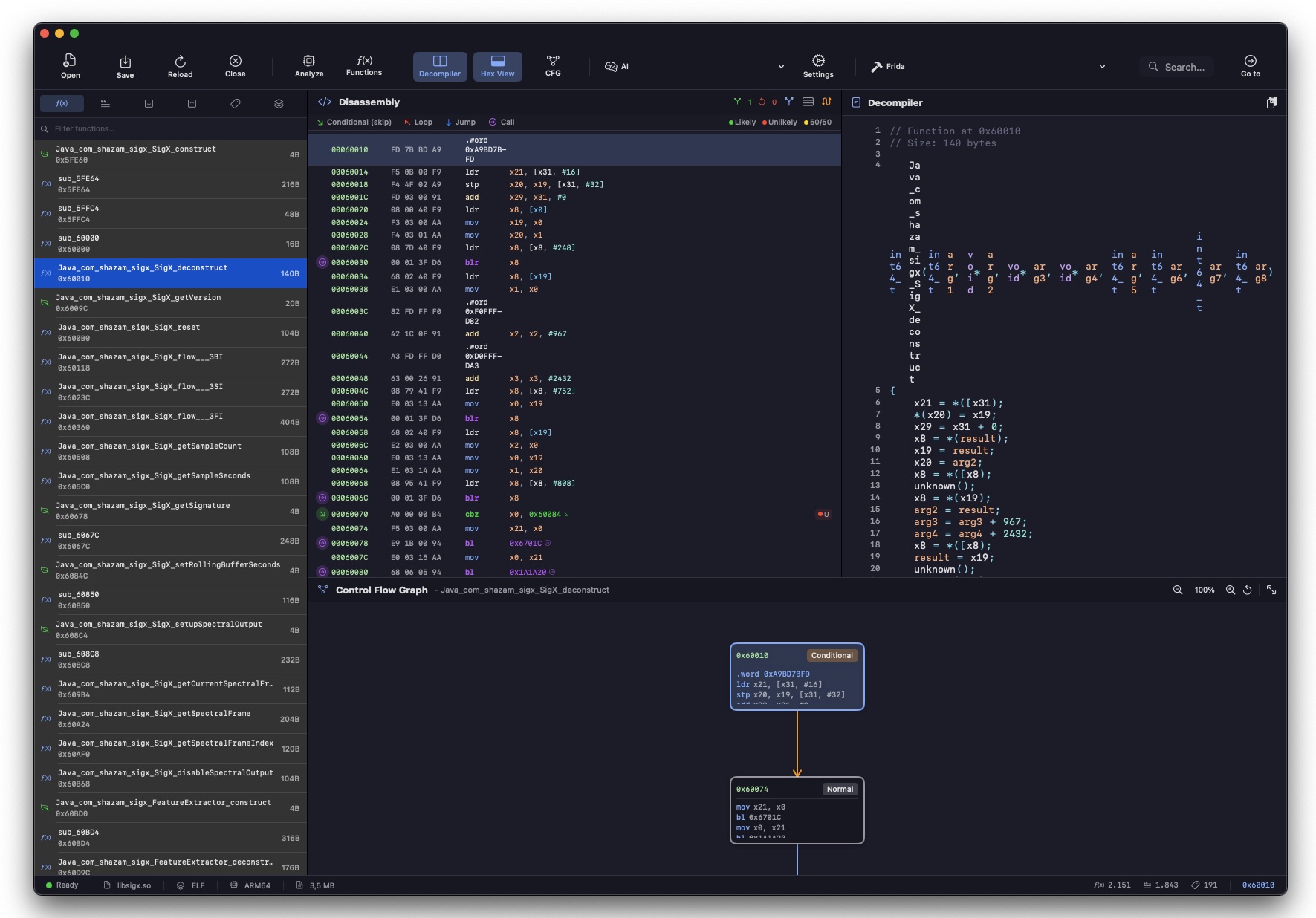
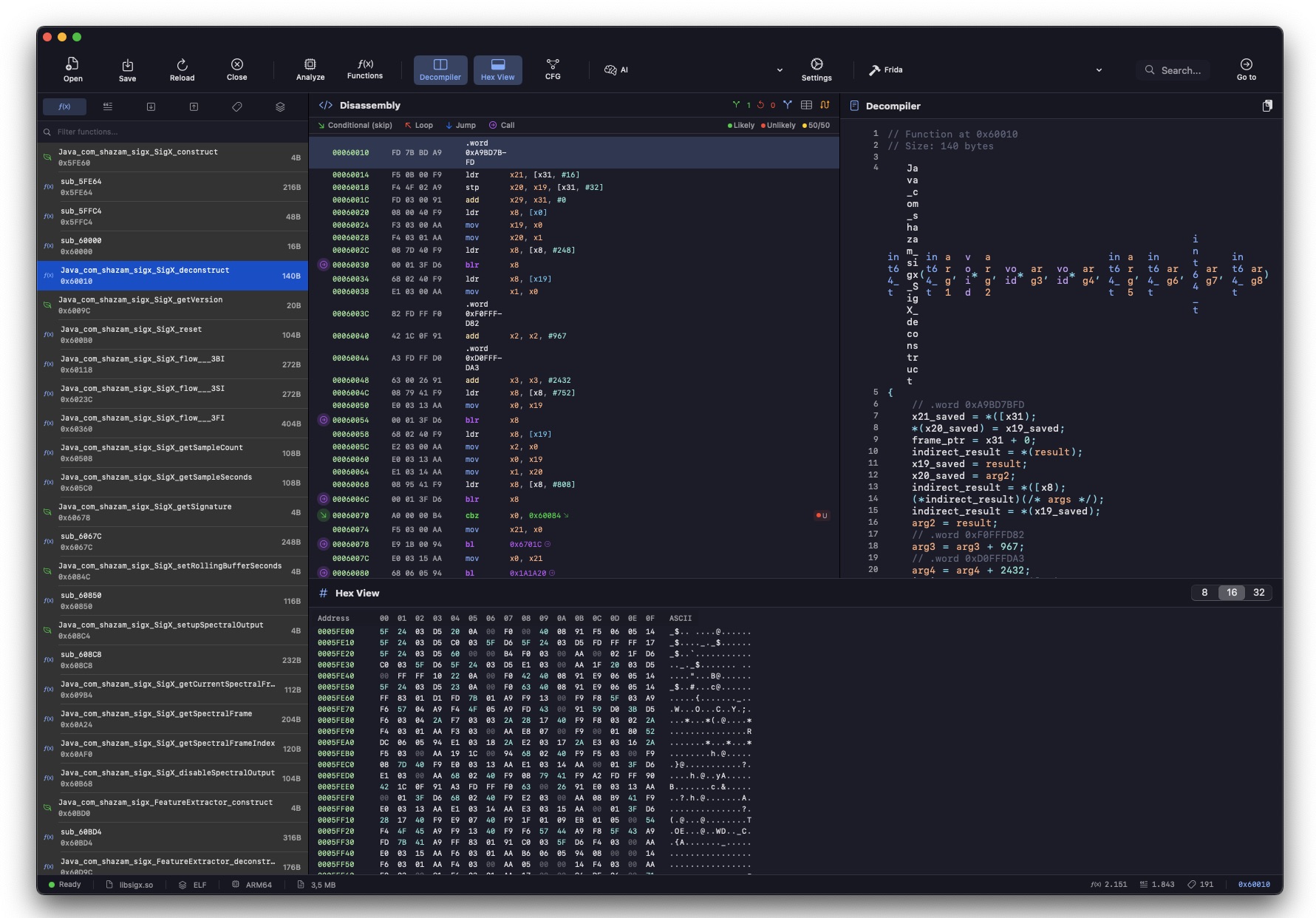
La classe Signature
Dalla decompilazione di Signature.smali emerge la struttura esatta del fingerprint inviato al server:
Il protocollo HTTP ricostruito
Dalla catena di interceptor OkHttp decompilata (H9/a, H9/b, H9/c, H9/e), ricostruisco la request completa:
Lo script Python
Ora so cosa manda l'app. Ma non riesco a farglielo mandare per davvero, perché libsigx.so crasha sull'emulatore. Allora cambio approccio: se conosco il protocollo, posso replicarlo. Esiste una libreria Python, shazamio, che implementa il fingerprinting e parla direttamente con i server di Shazam. Niente telefoni, niente emulatori, niente Frida. Solo Python, un file audio e una POST.
Funziona. La response è identica a quella che riceverebbe l'app. Tre righe di Python e ho il protocollo completo: fingerprint generato, request inviata, response con 12 match candidati, metadata, copertina, link Apple Music. Tutto.
Il fingerprint è dentro il campo uri della request: un blob binario (Protobuf serializzato, poi Base64) di ~100-500 byte. Contiene gli hash della constellation map generati dal motore di fingerprinting. Tutto il resto (timestamp, timezone, audioSource) sono metadati. Quei ~500 byte sono tutto ciò che serve per identificare una canzone tra 70 milioni.
Ora ho il protocollo, la response, la struttura dell'app decompilata. Ma la domanda resta: cosa c'è in quei 500 byte? Come fa il motore a ridurre 5 secondi di casino in un'impronta che identifica una canzone su 70 milioni? Per capirlo, serve la matematica.
// Il Suono è Solo Numeri
Sezione 03. Campionamento e digitalizzazioneIl suono è una variazione di pressione nell'aria. Il microfono la converte in tensione elettrica. Il convertitore ADC la trasforma in numeri. Fine della magia analogica. Da qui in poi è tutta matematica.
Shazam campiona a 44100 Hz, mono, 16 bit PCM. Significa 44100 misurazioni al secondo, ciascuna un intero a 16 bit (valori da -32768 a +32767). In 5 secondi di registrazione: 44100 × 5 = 220500 numeri. Circa 430 KB di dati grezzi. Tutto quello che serve.
Ma perché proprio 44100? La risposta è nel teorema di Nyquist-Shannon: per catturare fedelmente un segnale, la frequenza di campionamento deve essere almeno il doppio della frequenza massima da rappresentare.
Teorema di Nyquist-Shannon: la frequenza massima catturabile
L'orecchio umano arriva a circa 20000 Hz (in teoria, in pratica dopo i 30 anni si perde progressivamente). 44100 Hz copre tutto lo spettro udibile con margine. La iena dice che il mio udito si ferma a 14000 Hz dopo anni di concerti. Nyquist conferma: sto perdendo 6000 Hz di informazione. Ma per Shazam non importa, perché le frequenze utili per il riconoscimento musicale stanno quasi tutte sotto i 5000 Hz.
PCM 16 bit mono: il formato più semplice possibile. Nessuna compressione, nessuna perdita. Ogni campione è un numero intero che rappresenta l'ampiezza istantanea del segnale. La risoluzione dinamica è \(20 \cdot \log_{10}(2^{16}) \approx 96\) dB, più che sufficiente per catturare musica in qualsiasi ambiente.
Nel grafico qui sopra vedete un segnale musicale simulato (mix di frequenze) e lo stesso segnale immerso nel rumore di un ristorante. A occhio non si distingue niente. Ma le frequenze originali sono ancora lì dentro. Servono gli strumenti giusti per tirarle fuori.
// Fourier: Scomporre il Caos
Sezione 04. Dalla forma d'onda allo spettrogrammaIl segnale nel dominio del tempo è un casino. Un muro di numeri che salgono e scendono. Per trovare le note musicali serve un cambio di prospettiva radicale: passare dal dominio del tempo al dominio delle frequenze.
Questo è esattamente quello che fa la Discrete Fourier Transform (DFT). Prende un blocco di campioni temporali e li decompone nelle sinusoidi che li compongono. Ogni frequenza presente nel segnale diventa un picco nello spettro.
Discrete Fourier Transform: da N campioni temporali a N coefficienti frequenziali
In pratica si usa la FFT (Fast Fourier Transform), l'algoritmo di Cooley-Tukey che calcola la DFT in \(O(N \log N)\) invece di \(O(N^2)\). Con \(N = 1024\) campioni per finestra, la FFT viene calcolata centinaia di volte al secondo.
Ma una singola FFT ti dice quali frequenze ci sono, non quando appaiono. La musica cambia nel tempo. Serve una FFT che scorre lungo il segnale: la Short-Time Fourier Transform (STFT).
STFT: FFT su finestre scorrevoli. m = indice temporale, H = hop size, w[n] = finestra
La funzione finestra \(w[n]\) (Hann, Hamming, o simili) evita artefatti ai bordi del frame. L'hop size \(H\) determina la sovrapposizione: con \(N = 1024\) e \(H = 512\), ogni finestra si sovrappone al 50% con la precedente.
Il risultato è lo spettrogramma: una mappa 2D dove l'asse X è il tempo, l'asse Y è la frequenza, e il colore (o intensità) è la potenza spettrale.
Power Spectrum: l'intensità energetica ad ogni punto tempo-frequenza
Se Fourier esistesse per le conversazioni, scopriremmo che la frequenza dominante della iena è "non mi ascolti mai" a circa 3000 Hz, con armoniche a "lo dico sempre" e "ecco, l'avevo detto". Un segnale stazionario con zero varianza.
Insight chiave: Lo spettrogramma è la rappresentazione fondamentale su cui Shazam lavora. Ma non usa tutto lo spettrogramma, sarebbe troppo denso e troppo sensibile al rumore. Il passo successivo è estrarre solo i picchi: i punti di massima energia locale. Questi picchi sono le "stelle" nella constellation map.
// La Mappa delle Stelle
Sezione 05. Constellation Map, l'intuizione genialeSiamo nel 1999. Avery Li-Chun Wang, ingegnere a Stanford, ha un'idea che diventerà un brevetto da miliardi: e se invece di confrontare interi spettrogrammi, confrontassimo solo i picchi spettrali?
L'idea è brutalmente semplice. Nello spettrogramma, i punti di massima energia locale (le note dominanti, gli attacchi, le percussioni) sono stabili. Anche se aggiungi rumore, riverbero, distorsione, i picchi non si spostano. Cambiano di ampiezza, ma la loro posizione nel piano tempo-frequenza resta quasi identica.
Questi picchi, estratti dallo spettrogramma e plottati come punti su un piano (tempo, frequenza), formano una constellation map, una mappa delle stelle sonore. Ogni canzone ha la sua costellazione unica.
Ogni punto nel grafico è un landmark: un massimo locale nello spettrogramma. In 5 secondi di audio, Shazam ne estrae tipicamente 30-60. Pochi punti, ma sufficienti.
I picchi sono come le stelle: stabili. Come i punti che la iena segna mentalmente ogni volta che dimentico qualcosa. Una constellation map della mia inadeguatezza. Persistente, robusta al rumore, impossibile da cancellare.
Dall'ancora al target: le coppie hash
Un singolo picco non basta per identificare una canzone. Troppi falsi positivi. L'innovazione di Wang è usare coppie di picchi: un anchor point e un target point, collegati da una relazione tempo-frequenza.
Fingerprint hash: tre parametri, un indirizzo univoco nel database
Ogni coppia genera un hash compatto (tipicamente 32 bit) che codifica tre informazioni: la frequenza dell'ancora, la frequenza del target, e il delta temporale tra i due. Questo hash è l'impronta digitale, il fingerprint.
| Parametro | Valore tipico | Ruolo |
|---|---|---|
f_anchor |
10 bit (~0-5000 Hz) | Frequenza del punto ancora |
f_target |
10 bit (~0-5000 Hz) | Frequenza del punto target |
Δt |
12 bit (~0-4 secondi) | Differenza temporale tra i due punti |
| Hash totale | 32 bit | ~4.3 miliardi di indirizzi possibili |
Insight chiave: Con 32 bit di hash e ~70 milioni di canzoni nel database, ogni bucket contiene in media poche decine di entry. La ricerca è O(1), tempo costante. Non serve confrontare il campione con tutte le 70M canzoni. L'hash ti porta direttamente ai candidati.
// Il Match: Trovare l'Ago nel Pagliaio
Sezione 06. Offset histogram e significatività statisticaHai catturato 5 secondi di audio. Ne hai estratto ~200 hash. Li hai inviati al server. Il database ha restituito migliaia di candidati, canzoni che condividono almeno un hash con il tuo campione. Come scegli quella giusta?
La chiave è l'allineamento temporale. Se il tuo campione corrisponde realmente a una canzone nel database, allora tutti gli hash che matchano devono essere coerenti nel tempo. Se il tuo campione inizia al secondo 95 della canzone, tutti gli hash devono puntare a offset ~95.
Offset histogram: il picco nel conteggio degli offset identifica il match
In pratica: per ogni canzone candidata, calcoli l'offset temporale di ogni hash che matcha. Poi costruisci un istogramma. Se c'è un vero match, l'istogramma avrà uno spike pronunciato ad un singolo valore di offset. Se è un falso positivo, gli offset saranno distribuiti uniformemente.
La probabilità che \(k\) hash su \(B = 2^{32}\) bucket collidano per caso tutti allo stesso offset è astronomicamente bassa:
Con 5+ hash allineati, la probabilità di errore è trascurabile
La response che abbiamo catturato aveva 12 match candidati, tutti con offset coerente intorno a 95 secondi. Non è un caso: è la firma matematica di un match certo.
Insight chiave: Il genio del sistema è che non serve un match perfetto. Bastano 5-10 hash allineati sullo stesso offset per avere certezza statistica. Questo è il motivo per cui funziona nel rumore: anche se il 70% degli hash va perso a causa del casino del ristorante, il 30% rimanente è più che sufficiente.
// La Pipeline Completa
Sezione 07. Da onda sonora a "I Will Always Love You" in 5 secondiRicapitoliamo il flusso completo. Dal momento in cui premi il pulsante al momento in cui vedi il titolo sullo schermo:
Nel caso specifico di Shazam (dalla decompilazione dell'APK, sezione 02), la pipeline include anche una fase di feature extraction neurale: due modelli PyTorch (crema.pte e crepe.pte, ~1.9 MB ciascuno) che estraggono caratteristiche melodiche e di pitch. Questo è un'evoluzione rispetto al paper originale del 2003: il core resta la constellation map, ma le reti neurali aggiungono robustezza.
I dati finali vengono serializzati in Protobuf, codificati in Base64, e inviati come campo uri nel JSON della request. Il formato è data:audio/vnd.shazam.sig;base64,....
In 5 secondi: 220500 campioni → ~430 frame FFT → ~50 picchi → ~200 hash → 1 request HTTP → 12 match candidati → titolo sullo schermo. E la iena nemmeno se ne è accorta. (Spoiler: se ne è accorta eccome.)
// La Response: 12 Match Candidati
Sezione 08. Anatomia della risposta di amp.shazam.com
La response JSON di Shazam per "Flowers", catturata riproducendo il protocollo via shazamio, contiene 12 match candidati e un oggetto track con tutti i metadati.
I match candidati
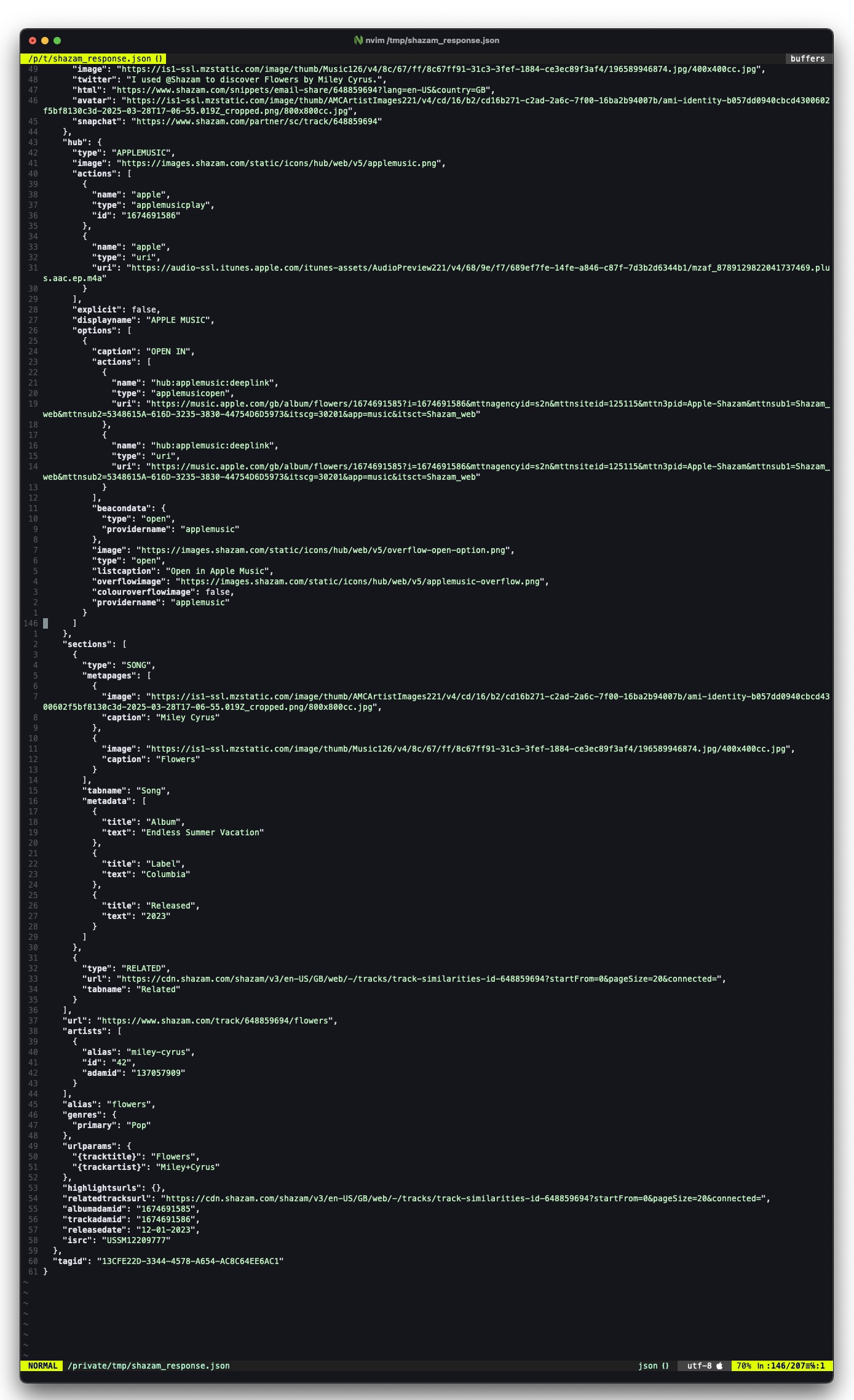
Cosa significano i campi
| Campo | Tipo | Significato |
|---|---|---|
id |
String | ID della traccia nel database Shazam (diversi ID = diverse release/versioni) |
offset |
Float (sec) | Punto esatto nel brano originale dove il campione combacia. ~95s = il campione era al minuto 1:35 |
timeskew |
Float | Deviazione temporale tra campione e originale. Vicino a 0 = match preciso |
frequencyskew |
Float | Deviazione in frequenza (pitch shift). 0 = stessa tonalità dell'originale |
isrc |
String | International Standard Recording Code, identificativo univoco mondiale della registrazione |
12 candidati, ma guardate gli offset: vanno da 87.8 a 143.3 secondi. Il grosso si concentra intorno a 95 secondi. Questo è l'offset histogram in azione: i match con offset coerente sono il segnale, il resto è rumore. I diversi id corrispondono a versioni diverse della stessa canzone nel database (single, album, remix, versione internazionale).
Il timeskew è particolarmente interessante: valori dell'ordine di \(10^{-4}\) indicano una deviazione temporale di 0.01%. La frequencyskew cattura eventuali variazioni di pitch, utile se la canzone è riprodotta leggermente accelerata o rallentata. Nel ristorante, con gli altoparlanti normali, entrambi i valori sono vicini a zero. Tutto torna.
Insight chiave: La response include anche l'URL della preview audio su Apple Music (un file .m4a), la copertina dell'album, i link per Snapchat e Twitter, e l'adamid di Apple Music. Shazam non è solo riconoscimento, è una pipeline di monetizzazione che converte 5 secondi di audio in un potenziale acquisto su iTunes.
// Perché Funziona nel Casino
Sezione 09. La matematica della robustezza al rumoreIl ristorante di San Valentino. 50 persone che parlano. Posate su ceramica. La macchina del caffè. La iena che dice "hai rimesso via quel telefono?". Eppure Shazam trova la canzone. Come?
La risposta sta nella natura del rumore ambientale rispetto alla musica. Il rumore di un ristorante è a banda larga: copre tutte le frequenze in modo relativamente uniforme. Le voci umane occupano la banda 300-3000 Hz. I piatti e le posate generano impulsi transitori brevi.
La musica, invece, ha struttura: note a frequenze discrete, armoniche a multipli interi della fondamentale, pattern ripetitivi nel tempo. Nello spettrogramma, la musica appare come linee orizzontali (note tenute) e punti brillanti (attacchi). Il rumore è una nebbia uniforme.
Signal-to-Noise Ratio: in un ristorante tipico, SNR ≈ -5 a +5 dB
Con un SNR di 0 dB (segnale e rumore alla stessa potenza), potresti pensare che sia impossibile distinguere qualcosa. Ma i picchi spettrali della musica sono localmente molto più intensi del rumore di fondo. Anche se globalmente il rumore ha la stessa energia della musica, localmente, nei bin di frequenza dove c'è una nota, il segnale domina.
Questo è il motivo per cui la constellation map funziona: i picchi sono massimi locali. Il rumore alza il pavimento, ma non sposta i picchi. Le stelle restano visibili anche con la nebbia.
Il rumore del ristorante distrugge il 50-70% degli hash. Ma il match richiede solo 5-10 hash allineati. Se il campione pulito produce ~200 hash, e il rumore ne lascia in piedi 60-100, la probabilità di match resta altissima. La ridondanza combinatoriale è il segreto: il sistema è progettato per funzionare con dati parziali.
Con 10+ hash sopravvissuti al rumore, la probabilità di match converge a 1
Il rumore del ristorante è a banda larga, copre tutte le frequenze uniformemente. Come il brusio della iena quando guardo il telefono a cena: costante, onnipresente, ma non abbastanza strutturato da spostare i picchi del segnale che sto cercando. Shazam ignora il rumore e trova la musica. Io dovrei imparare a fare lo stesso. (La iena, se legge questo, mi ammazzerà. Ma con un timeskew vicino a zero, il che mi dà almeno la soddisfazione della precisione.)
Insight chiave: Shazam funziona fino a circa -5 dB di SNR (rumore doppio rispetto al segnale). Il paper originale di Wang (2003) riporta un tasso di riconoscimento del 95% in condizioni "moderatamente rumorose". Il ristorante di San Valentino, a posteriori, era ben dentro il range operativo.
// La Magia è Solo Matematica
Sezione 10. ConclusioneRicapitoliamo. In 5 secondi, il telefono ha:
- Catturato 220500 campioni a 44100 Hz
- Applicato la STFT con finestra Hann su ~430 frame sovrapposti
- Estratto ~50 picchi spettrali (la constellation map)
- Generato ~200 hash combinatoriali da coppie di picchi
- Serializzato tutto in ~500 byte di Protobuf + Base64
- Inviato una POST a
amp.shazam.com/match - Ricevuto 12 match candidati con offset a ~95 secondi
- Mostrato titolo, artista, copertina e link Apple Music
Nessuna intelligenza artificiale magica (anche se i modelli CREMA/CREPE aggiungono il loro). Nessuna comprensione del significato musicale. Solo Fourier che decompone onde, picchi che resistono al rumore, hash che permettono ricerche in O(1), e statistica che rende i falsi positivi impossibili.
La prossima volta che siete in un ristorante rumoroso e Shazam vi dice il titolo della canzone in 5 secondi, ricordatevi: non è magia. È un signore francese del 1807 che ha capito che qualsiasi segnale si può scomporre in sinusoidi, un ingegnere di Stanford che nel 1999 ha pensato di usare solo i picchi, e un bel po' di hash table.
5 secondi. 220500 campioni. 50 picchi. 200 hash. 12 match. 1 canzone. Zero magia. Fourier ha fatto il lavoro pesante. Avery Wang ha avuto l'intuizione. E io ho finalmente scoperto cosa suonava al ristorante mentre la iena mi guardava male. 26 anni di matrimonio sopravvissuti a Nyquist, alla constellation map e a un telefono tirato fuori a San Valentino. Se il nostro rapporto fosse un segnale, avrebbe un SNR bassissimo ma evidentemente abbastanza picchi stabili per un match. La robustezza non sta nella potenza del segnale. Sta nella struttura.
Signal Pirate